Trusted computing can depend on asymmetric cryptography algorithms to assure the integrity of protected data
By David Sheets
ASHBURN, Va. – There are three general categories of cryptographic algorithms commonly employed in trusted computing: secure hashing, symmetric cryptography, and asymmetric cryptography.
Asymmetric algorithms enable systems designers to use a pair of keys to access data. One key signs or encrypts data, while the other verifies or decrypts data.
This pairing of keys provides the opportunity for novel cryptographic operations when compared to more traditional symmetric algorithms. Normally, in asymmetric cryptography the key pairs are called the “private-key," or one that is securely stored and not-shared, and the “public-key," a matching key that is freely shared with others.
Asymmetric cryptography
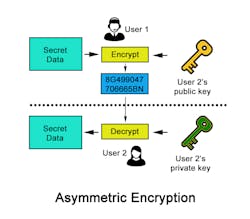
Asymmetric cryptographic algorithms enable several use cases. One is personalized encryption, where the sender encrypts data using the public key. Only the matching private-key can decrypt it, which protects the data’s confidentiality against external attackers.
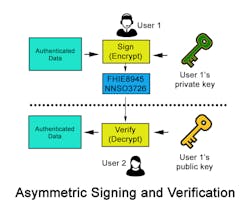
Digitally signing of data also uses asymmetric cryptography by processing the data to be signed using the private-key of the sender. Once the other system receives the data, it can use the already shared corresponding public-key to verify the signing.
What’s more, the public-key can verify data authenticity after signing This use case fails, however, if the does not maintain the private key's confidentiality securely. Most digital signing algorithms do not work directly with the data at signing, but instead operate on a hash of the data to sign. This approach enhances performance as most algorithms operate with large numbers, making it infeasible to process a large amount of data directly converted into a number.
A third use case for asymmetric cryptography involves key agreement protocols, which use asymmetric algorithms because of the increased speed of symmetric algorithms. The slower asymmetric cryptographic operations enable initial key agreements and then use a secret key for fast symmetric cryptographic operations to protect the confidentiality of communications.
Key agreement protocols are appropriate when both parties know the other’s public-key from the start. Each party computes a shared secret value using his own private-key and the other party’s public-key. Using secure hashing algorithms to derive additional keys may protect the shared secret value further.
Asymmetric cryptographic algorithm attackComputer hackers can use several types of attacks on asymmetric algorithms. In most of these attacks, the attacker already knows the public portion of a key pair and searches for the corresponding private-key. A successful attack would enable the attacker to sign non-authentic data, or decrypt data encrypted for that specific recipient.
Brute-force attack
The most straightforward type of attack against asymmetric algorithms is by brute force. Most asymmetric cryptographic algorithms defend themselves from this type of attack by operating on very large numbers, which makes the search space of possible keys sufficiently large to make a successful brute force attack infeasible.
Related: Cryptography in trusted computing: an introduction to secure hashing
Man-in-the-middle attacks
A man-in-the-middle attack attempts to put the attacker in the middle of some portion of a key exchange operation, enabling them to fool both sides into reaching a key agreement with the attacker instead of with the expected partner. These sorts of attacks rely on insufficient protection during the sharing of public-keys. The use of Public Key Infrastructure (PKI) can help prevent these sorts of attacks in distributed environments. PKI provides a trusted authority that can securely authenticate and distribute the public-keys of individual participants.
Side-channel attacks
Side channel attacks also can be effective against asymmetric cryptography by targeting information leaked due to the implementation details of the algorithm and the specifics of the key used. Normally, this attack analyzes some side channel of information over several cryptographic blocks to determine the secret portion of the key pair.
Examples of the type of information that can be analyzed are timing information; cache hits and misses; and power usage.
The first asymmetric cryptographic algorithms were developed in the early 1970s. The first published work was the Diffie-Helman (DH) Key Exchange algorithm, which was based on the difficulty of reversing exponentiation in a finite field.
The next set of asymmetric algorithms to be published was RSA, named after the three authors Ron Rivest, Adi Shamir, and Leonard Adleman. RSA depends on the mathematical difficulty of factoring large prime numbers.
Over the years, RSA has increased key sizes to maintain security while keeping up with technological progress. In response to this trend, elliptic curve cryptography (ECC) has come into prominence. ECC depends on the mathematical difficulty of finding a discrete logarithm for a pair of points on an elliptic curve. Both RSA and ECC can be used as the foundation for one-way encryption or a signing/verification algorithm.
Diffie-Hellman (DH) key exchange is designed to reach agreement on a common shared secret key when communicating over a non-secure channel. It does not provide any authentication, so it is vulnerable to man-in-the-middle attacks when not paired with additional protection.
The DH protocol is described in detail in the IETC RFC 3526 standard. In general, it works by having each party agree on a non-secret base and a non-secret modulus. When operating mathematical functions with a modulus, all results are constrained between 0 and the modulus value.
If a mathematical operation result is over the modulus, the modulus is subtracted from the result until it is within the acceptable range. For example, 57 mod 10 = 7 (aka 57 – 10 – 10 – 10 – 10 – 10 = 7). With DH, each party raises the non-secret base to his own secret exponent constrained to the modulus, and then sends the result.
Each side then computes the received value raised to his own secret constrained to the modulus value. Because both sides raised the same base to both of the (secret) exponents constrained to the modulus, they now share the same secret value -- one that is hard to compute because reversing exponentiation in the finite field of the modulus is mathematically difficult.
The extent of the mathematical difficulty is dependent on ensuring that large enough values are chosen for the modulus and for both secret exponents.
RSA asymmetric algorithm
RSA refers to a set of protocols, all based on the mathematical difficulty in factoring large prime numbers. RSA algorithms are categorized based on the bit-length of the modulus (also called the “key size”). Early implementations of RSA used the smaller key sizes of 128 or 256 bits, which today can be broken in seconds.
Current implementations typically use 2048 or 4096 bit keys, with most recommendations leaning towards 4096 bit keys lengths where possible.
RSA public/private-keys pairs can be used for encryption, signing and verification, or key agreement. Encrypting a message involves converting the message to a number, which then is raised to the recipient’s public-key exponent modulus n. The recipient can retrieve the plain text by raising the received message to the private-key exponent modulus n.
The sender signs the message by converting it to a value, and raising that value to the sender’s private-key modulus n. The recipient then raises the signature to the sender’s public-key modulus n. If the result matches the sent message, then the signature was genuine.
Related: Lowering the costs of encrypted data storage in trusted computing
ECC provides an alternative to RSA by helping address the performance of the mathematical operations that compute the RSA exponentiation for larger key sizes.
ECC relies on a completely different mathematical principle by operating on numbers that exist on a defined elliptic curve -- most often by using the named curves recommended in the NIST FIPS 186-4 Digital Signature Standard (DSS).
Curves in the DSS Appendix D are named according to the size of the prime in bits, with larger values indicating a larger set of possible points. The larger the set, the greater the mathematical difficulty in breaking the math underlying the cryptographic algorithm. Named elliptic curves in DSS include P-192, P-224, P-256, P-384, and P-521.
In ECC, public/private-key pairs represent two values. The private-key is an integer in the range of the prime value. ECC calculates the corresponding public-key mathematically by using a generator point, the private-key integer, and the concept of addition within the finite field of the elliptic curve.
Once it chooses an appropriate curve and generates public/private-key pairs, the key pairs can be used in a key exchange protocol or Elliptic Curve Diffie-Hellman Key Exchange (ECDH), or to digitally sign data using the elliptic curve digital signature algorithm (ECDSA).
Related: A guide to international authorities for global trusted computing standards certification
ECDH is similar to the DH protocol, but operates on points on the curve instead of with exponents. In ECDH, each side keeps his private-key secret and shares their public-key, but then generates a shared secret point on the elliptic curve using their own private-key and their counterpart’s public-key.
ECDSA is a variant of DSA that uses ECC instead of modular exponentiation. ECDSA requires a random value for each signature. One potential weakness is the reuse of the same random value with the same signature keys.
Implementations that fail to provide sufficiently random values can potentially be compromised because of the underlying math of the signature algorithm. For example, this vulnerability calculated the private-key to authorize games on the PlayStation-3. Correct implementations of ECDSA are still secure, but should use algorithms properly to avoid unnecessary vulnerabilities.
Current recommended key lengths
The Committee on National Security Systems (CNSS) Policy 15 Appendix B specifies a set of recommended key sizes for protecting national security systems. For asymmetric cryptographic algorithms, the publication recommends the following minimum sizes: curve P-384 for ECC; and a minimum of 3072 bit for RSA and DH key exchange.
Quantum computers, based on quantum bits (qubits), operate very differently from traditional Von Neumann architecture computers, and have significant implications for cryptography.
While traditional machines require 2^n bits to represent all possible values of a key of n-bits, a quantum computer, with n qubits, has a probability for those qubits to enter each of the possible key values.
This means that quantum computers can attack many mathematical problems that are infeasible with traditional computers. The bad news is that quantum computers can potentially solve integer factorization, exponentiation, and discrete logarithm problems, which are the mathematical underpinnings of RSA, ECC, DSA, and DH.
Fortunately, no quantum computer has been built with sufficiently large numbers of qubits to solve today's keys sizes reasonably. Still, the days of using existing asymmetric cryptographic algorithms may be numbered because of the fast rate of progress.
David Sheets is senior principal security architect at Curtiss-Wright Defense Solutions. Contact him by email at [email protected].
