Trusted computing and the challenges of cryptographic algorithms in quantum computing
By David Sheets
ASHBURN, Va. – At its core, quantum computing is very different from a traditional computer. The quantum computer operates on qubits, using quantum gates and measurements, rather than operating on bits per a Von Neuman architecture -- using memory and a processing unit made up of digital gates.
A qubit is not binary. It does not simply encode a 1 or a 0 as a bit does. Instead a set of n qubits encodes a superposition of 2^n possible quantum states. This means that while a traditional digital computer operating on 32-bits only can process one 32-bit value at any given time, a quantum computer with 32-qubits can look simultaneously at the probabilities of all possible 32-bit value combinations.
Quantum computing has several https://www.militaryaerospace.com/trusted-computing challenges. A quantum computer processes a particular algorithm by configuring the set of quantum gates, and initializing the values of the qubits. Taking a measurement causes the quantum states to resolve, and users can measure an actual state of the qubits. For example, once the quantum states resolve in a 32-qubit system, it is no longer in an unknown set of the 2^32 possible combinations, but has resolved to a single possible solution.
Because a quantum computer works with quantum states, each value is often only probabilistic in nature. Normally, to determine a result with sufficient accuracy, a quantum computer runs several times, re-initializing the system, configuring qubits, and then measuring a state. Each subsequent measurement records as a potential result. Users then can analyze these sets of results to determine which of the results most likely are correct.
Quantum computing and cryptography
Quantum computers have a couple of significant influences on the current state of cryptographic algorithms. The first is the ability of quantum computers to implement Grover’s algorithm. Using Grover’s algorithm a quantum computer can find the input to a black box function that results in a given output, and can do so in half the time of traditional brute-force algorithms. This means that protection from symmetric key algorithms reduces effectively by 50 percent. To mitigate against this threat, it’s crucial to ensure that the key-length of any symmetric cryptographic algorithms take this halving effect into account. Doubling the key lengths of symmetric cryptographic algorithms would suffice to protect against Grover’s algorithm running on sufficiently robust quantum computers.
The second influence results from the ability of quantum computers to run Shor’s algorithm efficiently. Shor’s algorithm can solve the underlying integer factorization problems on which RSA and Diffie-Hellman cryptography are based. Unfortunately for trusted computing, Shor’s algorithm also can solve the discrete logarithm problem on which the Elliptic Curve Diffie-Hellman algorithm is based. Compared to the threat of Grover’s algorithm to the effectiveness of symmetric algorithms, mitigating against Shor’s algorithm is much harder and will require substantial reworking of trusted computing systems.
The good news is that quantum computers that can operate on sufficiently large number of qubits don’t yet exist. It’s important though to understand that these machines are coming, and that their arrival will render the three most used asymmetric algorithms obsolete. Today, cryptographers are working hard to determine the best ways to ensure trusted computing systems can continue to maintain security and trust well into the future.
Hash algorithms for signatures
There are some algorithms that resist known quantum computer-based attacks that already are available and in use. Many of these algorithms can help bolster security in the face of quantum computing systems. For example, hashing algorithms appear just as able to resist attacks from quantum computers as they are from traditional computers. Some hashing algorithms, in fact, can help defend against quantum computer based attacks just as well as asymmetric algorithms can.
In many systems, asymmetric algorithms sign data, with the private key held outside of the system. The public key then can embed in the system and verify authenticity prior to operation. Since these systems keep the private key outside of the system, they resist attackers obtaining the private key and signing their own data. Hashing algorithms can be the basis for other data structures that can provide similarly secure authentication capabilities to systems.
Lamport Signature single-use algorithm
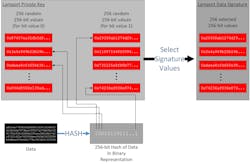
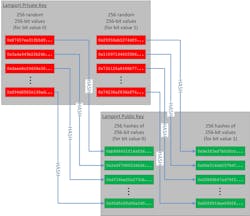
As an example, the Lamport Signature algorithm is based on hashing algorithms and allows a secure one-time-use public-private key pair. In the Lamport Signature algorithm the signer picks a hash algorithm, such as SHA-256. Based on the selected hash algorithm, the signature can support 256-bit signatures. The signer then generates 256 pairs of 256-bit numbers, which generates a total of 512 256-bit numbers. These random numbers serve as the private key.
This approach hashes each of the resulting 512 numbers to generate a set of 512 256-bit hashes, which becomes the public key. The system signs data by hashing, which generates a 256-bit value. The system then chooses one of the two random values from the set of saved private-key values. If a bit is 1, the first value is chosen, if a bit is 0, the second value is chosen. This selection process repeats for all 256-bits of the hashed value of the data, moving through the set of 256 256-bit private key pairs. The final signature passed with the data is the set of selected 256 256-bit values.
To verify the signature, the recipient takes all 256 of the 256-bit values from the signature and hashes each value, resulting in 256 256-bit hash values. The recipient then goes through the pairs of 256 256-bit values in the public key and selects one from each pair, as the signer did, based on the bits of the hash of the data. The data authenticates if the selected values from the public key hashes match the calculated hashes of the signature.
While this signature scheme works, it requires large signatures, and requires new one-use public keys, for every data item it authenticates. Using it in a system requires infrastructure to deliver new one-use public keys securely. This is necessary to maintain security, or the system must come loaded with a very large preinstalled set of public keys.
Merkle Tree Signatures
Another approach for protecting against quantum computer attacks uses the Merkle Signature Scheme, which builds on a one-time signature scheme, such as the Lamport Signature algorithm. The Merkle Signature Scheme generates a set number of one-time-use public-private key pairs. Each of the public keys is then hashed, and the resulting hash becomes the leaf in a Merkle Tree.
Related: Cryptography in trusted computing: an introduction to secure hashing
This binary Merkle Tree consists of leaf data nodes, where each parent node is a hash of the concatenation of the two children nodes. As with the Lamport Signature algorithm, the signer generates a private key using one of the previously unused public-private key pairs from the Merkle Tree leaf nodes. The signer then also appends the set of sibling nodes going up the Merkle Tree from the selected leaf node.
This enables the recipient to verify that the received signature is actually part of the Merkle Tree. All of this means that instead of preinstalling all 2^n public signatures initially generated as part of the Merkle Tree, the public signatures can be sent out as needed, and verified as part of the Merkle Tree during the signature verification.
However, there are still caveats with using Merkle Trees -- namely all of the public-private key pairs need to be pre-generated. Also, there are a limited number of possible signatures that can be used based on the value of n chosen when the Merkle Tree is initially generated. However, for systems that require long term protection, these algorithms can provide security in the face of increasing quantum computing capabilities.
NIST post-quantum cryptography status
Given the serious concerns of using existing algorithms to sign and authenticate data well into the future, the National Institute of Standards and Technology (NIST) in Gaithersburg, Md., has initiated a process to select possible algorithms to replace currently available asymmetric cryptographic algorithms.
The first round of NIST’s evaluation has been completed and a status update was released in NIST IR 8240 on January 2019. The second-round standardization conference will be next month to refine the set of 26 algorithms selected from the 69 first round candidate algorithms. Of the 26 algorithms currently being analyzed, 17 are public-key encryption/key-establishment algorithms and 9 are digital signature algorithms.
There are categories of types of algorithms that are being developed. Most algorithms that made it to the second round use lattice-based cryptography, multivariate cryptography, or code-based cryptography. There was also one algorithm, based on a random walk over elliptic curves, which so far looks to be not susceptible to quantum computers.
While there are currently available implementations for each of these algorithms on the NIST website, since they are still under review, it doesn’t make much sense yet for most trusted computing systems to rely on these unproven algorithms. Industry should wait until further analysis has been completed.
It is important for those of us involved in trusted computing to keep an eye on the progress of NIST in their oversight of the analysis of the future of post-quantum cryptographic algorithms at https://csrc.nist.gov/Projects/Post-Quantum-Cryptography.
Based on currently available timelines from NIST, we can hope to have draft standards of algorithms available sometime between 2022 and 2024. At that point, to mitigate against the threat that quantum computing poses to data security, it will be our responsibility to help bring these algorithms into the trusted computing systems we develop and deploy.
David Sheets is senior principal security architect at Curtiss-Wright Defense Solutions. Contact him by email at [email protected].
